screen
screen を使って、sshを切っても処理を実行させたいので、
$ screen $ script/myapp_server.pl -r
という感じにする。
僕の場合は、script/myapp_server.pl以外に別の.plを走らせる必要があるので、
新しくCtrl+Shift+tとして、ssh接続し、
$ screen $ sample.pl
などとする。
まだよくわかってないが、
script/myapp_server.plを走らせたくなくなったら、どうするか?
複数走らせていて$screen -r ってすると以下のように出る。
$ screen -r There are several suitable screens on: 41412.pts-0.dti-vps-srv81 (2013年02月28日 07時33分57秒) (Detached) 42312.pts-3.dti-vps-srv81 (2013年02月28日 07時21分36秒) (Detached) 11432.pts-7.dti-vps-srv81 (2013年02月28日 07時20分56秒) (Attached) 58233.pts-0.dti-vps-srv81 (2013年02月28日 07時14分54秒) (Attached) Type "screen [-d] -r [pid.]tty.host" to resume one of them.
てな感じででてくるので、Detachedのやつの例えば、
$ screen -r 41412.pts-0.dti-vps-srv81
ってやるとさっき走らせたやつが開ける。
今日という日
強風だったのでTXのダイヤが乱れていた。
東京に行くときはやはり、時間に余裕を持っていかなければ、急な出来事に対応できないと思った。
千代田線も少し遅れていたようで、不安だった。
時間通りにことが進まないと不安になる。なので、余裕のある生活を送りたい。
何を言いたいのか分からなくなってきたので、この辺にして、眠りにつきたい。
こういう日記は、久しぶりに書いた気がするので、なぜか新鮮な気持ちである。
全く関係のない話だが、前にブログで手書き文字について議論したことを思い出すと、ブログに手書きのようなフォントがあったら、間違いなくこのブログはそのフォントを使いたい。
欲を言うならば、縦書きで小学生の作文みたいにしたら絶対に楽しいと思う。
主成分分析による手書き数字の復元
手書き数字について、主成分分析を行うことで、特徴抽出、画像の文字の復元することができる。
https://www.kaggle.com/c/digit-recognizer/data
のtrain.csvデータにheaderにlabel, pixel0 から pixel783まで定義されている。
train.csvを用いて、手書き数字の復元する。
どの数字でも良いのですが、今は0にする。0である手書き数字の標本数は4131である。
Xを の0である標本ベクトル(縦のp次元ベクトル)を横に標本数分並べる。
つまり、
とする。
このとき、の固有ベクトルは主成分ベクトルになる。(詳細は略)
固有値が大きい順に並べて、対応する固有ベクトルが第1主成分,第2主成分,...に対応する。
第1列X[,1]の画像を復元しようとおもったら、
とするとき
より、
が成立するので,
受信側が固有ベクトルを持っていれば、
送信側は、を送信すれば、受信側は、復元できることになる。
しかも、はそれほど多く取得しておく必要もない。
なぜなら、以下のように、画像の復元が少ない主成分(今は16,32,64,128)で復元できているからである。
今、n=4131で、m=16,32,64,128について、
が成立しているからである。




最後に、0の固有ベクトルを25個まで表示する。

所詮、PCAは2次の情報(相関)しか持っていないので、精度は悪い。
今度は、ICAを試すことにする。
お腹が痛くなってきたのでこの辺で。。
githubにコードを上げようと思ったけどやめた。
setwd("./Dropbox/R/handwritten") getwd() ## Read in data train <- read.csv("./data/train.csv", header=TRUE) train<-as.matrix(train) dim(train) #42000 785 ##Color ramp def. colors<-c('white','black') cus_col<-colorRampPalette(colors=colors) #16?i???ŕԂ? cus_col(256) ## Plot the average image of each digit par(mfrow=c(1,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n') all_img<-array(dim=c(10,28*28)) #NA??10*784?̍s???쐬 #all_img di0 = train[train[,1]==0,-1] di0mat=di0[-1,] dim(di0mat) #4131 784 di0.cor=cor(di0mat) di0.cor X=t(di0mat) dim(X) #p x n Xvar=function(X){ return((1/n)*rowSums(X))#各行の和 } xvar=Xvar(X) length(xvar) xvar#標本平均ベクトル n=ncol(X) n p=nrow(X) p #標本分散共分散行列の初期化 S=matrix(0,nrow=p,ncol=p) #S #(X[,i]-xvar)%*%t(X[,i]-xvar) for(i in 1:n){ S=S+(X[,i]-xvar)%*%t(X[,i]-xvar) } S=(1/n)*S S dim(S) eigen(S)$values eigen(S)$vectors[,1] length(eigen(S)$vectors[,1]) #p di=0 m=128 yvec=matrix(0,nrow=m,ncol=1) for(i in 1:m){ yvec[i]=t(eigen(S)$vectors[,i])%*%X[,1] #1番目の標本の第i主成分 } z<-array(X[,1],dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main="original data",col=cus_col(256)) n restorevec=matrix(0,nrow=p,ncol=1) for(i in 1:m){ restorevec=restorevec+yvec[i]*eigen(S)$vectors[,i] #1番目の標本の第i主成分 if(i==16||i==32||i==64||i==128){ z<-array(restorevec,dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main=i,col=cus_col(256)) } } #2番目の標本の復元################### m=128 z<-array(X[,2],dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main="original data",col=cus_col(256)) yvec=matrix(0,nrow=m,ncol=1) for(i in 1:m){ yvec[i]=t(eigen(S)$vectors[,i])%*%X[,2] #2番目の標本の第i主成分 } restorevec=matrix(0,nrow=p,ncol=1) for(i in 1:m){ restorevec=restorevec+yvec[i]*eigen(S)$vectors[,i] #1番目の標本の第i主成分 if(i==16||i==32||i==64||i==128){ z<-array(restorevec,dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main=i,col=cus_col(256)) } } #3番目の標本の復元################### m=128 z<-array(X[,3],dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main="original data",col=cus_col(256)) yvec=matrix(0,nrow=m,ncol=1) for(i in 1:m){ yvec[i]=t(eigen(S)$vectors[,i])%*%X[,3] #3番目の標本の第i主成分 } restorevec=matrix(0,nrow=p,ncol=1) for(i in 1:m){ restorevec=restorevec+yvec[i]*eigen(S)$vectors[,i] #1番目の標本の第i主成分 if(i==16||i==32||i==64||i==128){ z<-array(restorevec,dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main=i,col=cus_col(256)) } } #4番目の標本の復元################### m=128 z<-array(X[,4],dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main="original data",col=cus_col(256)) yvec=matrix(0,nrow=m,ncol=1) for(i in 1:m){ yvec[i]=t(eigen(S)$vectors[,i])%*%X[,4] #4番目の標本の第i主成分 } restorevec=matrix(0,nrow=p,ncol=1) for(i in 1:m){ restorevec=restorevec+yvec[i]*eigen(S)$vectors[,i] #1番目の標本の第i主成分 if(i==16||i==32||i==64||i==128){ z<-array(restorevec,dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main=i,col=cus_col(256)) } } #0の固有ベクトルを25個まで表示する########## par(mfrow=c(5,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n') l=5*5 for(i in 1:l){ z<-array(eigen(S)$vectors[,i],dim=c(28,28)) #28*28?̉摜?ɂ??邽?߁B z<-z[,28:1] ##right side up #??28??????1???ɁA??27??????2???ɁA.... image(1:28,1:28,z,main=i,col=cus_col(256)) }
デジタル画像(Handwritten)
http://bayesianbiologist.com/2012/08/13/the-essence-of-a-handwritten-digit/
で使われている
https://www.kaggle.com/c/digit-recognizer/data
のtrain.csvデータにheaderにlabel, pixel0 から pixel783まで定義されている。
28*28(=784)の手書き画像が42000個収録されている。
ETL形式より楽。
■
Integrate[Exp[-(s^2/2)]*Cosh[s], {s, -Infinity, Infinity}]
は、
s=seq(-5,5,,1000) plot(s,exp(-log(2)-2*log(cosh(s))),xlim=c(-5,5),ylim=c(0,0.8),type="l") par(new=T) plot(s,(1/sqrt(2))*exp(-sqrt(2)*abs(s)),xlim=c(-5,5),ylim=c(0,0.8),type="l") x=seq(-5,5,,1000) plot(x,f(x),xlim=c(-5,5),ylim=c(0,2),type="l") par(new=T) plot(x,dunif(x, min=-sqrt(3), max=sqrt(3), log = FALSE),xlim=c(-5,5),ylim=c(0,0.4),type="l") par(new=T) g = function(x) exp(-(1/2)*log(2*exp(1)*Pi)-(s^2/2)+log(cosh(s))) plot(x,g(x),xlim=c(-5,5),ylim=c(0,0.4),type="l")
最尤法によるICA(メモ)
https://docs.google.com/open?id=0Bzz10UZbU-i5WGctWWtQSERsaTg
https://docs.google.com/open?id=0Bzz10UZbU-i5aUNfU0UwWVpXcjQ
メモ:
勾配法を用いた最尤法による独立成分抽出は,お世辞にも推定できているとはいえない。
最尤法によるFastICAは,まあまあかな。
推定できたという、判断基準がほしい。
Schedule::Cron
foreachを使ってadd_entry すると指定した時間でちゃんと動かない。(即、jobが実行される)
#!/use/bin/perl use strict; use warnings; use Schedule::Cron; sub dispatcher{ print "ID: ", shift, "\n"; print "Args:","@_", "\n"; } sub job{ # 実行したい処理 print "job:$_[0]\n"; } my $cron = new Schedule::Cron(\&dispatcher); my @min = (54,55,56); foreach(@min){ $cron->add_entry("$_ 23 * * * ", \&job($_)); } $cron->run();
ひとつひとつadd_entryするとうまく行く。しかし、これでは、不便である。
デジタル画像処理

- 作者: 勝木健雄,蓬来祐一郎,金明哲
- 出版社/メーカー: 共立出版
- 発売日: 2011/11/23
- メディア: 単行本
- 購入: 2人 クリック: 10回
- この商品を含むブログ (4件) を見る
最初、自分でネットで調べてGTK+やImageMagicのインストールをしたのだが、うまく動いてくれなかった。
https://code.google.com/p/rimagebook/wiki/RImageBookInstallationというのがちゃんとあった。
これを参考にするだけだが、
EBImageのインストール
https://code.google.com/p/rimagebook/wiki/EBImageInstallation#Linux
のところで
$ sudo wget http://www.bioconductor.org/packages/devel/bioc/src/contrib/EBImage_3.11.2.tar.gz
$ sudo R CMD INSTALL EBImage_3.11.2.tar.gz
とせよとある。
しかし、すでに、3.11.2はなくEBImage_4.1.1.tar.gzだった。
単純に置き換えて、
sudo R CMD INSTALL EBImage_4.1.1.tar.gzとしたが、インストール出来なかった。
そこで、
$ sudo R
>source("http://bioconductor.org/biocLite.R")
>biocLite("EBImage")
>citation("EBImage")
とした。
biOpsなどを入れ、
$ sudo apt-get install subversion
$ sudo svn checkout http://rimagebook.googlecode.com/svn/trunk/ rimagebook-read-only
$ cd rimagebook-read-only/RImageBook
$ sudo bash ./build.sh
sudo R
library(RImageBook)
で
適当にhttps://code.google.com/p/rimagebook/wiki/DemoListから選んで、
例えば、demo(EdgeDetectionDemo)
とする。
TextRecognitionDemoは、手書き文字の認識であるが、ファイルが別に必要で、本に書いてあるところからダウンロードしてくる。
「ETL1C_01」というファイルをrimagebook-read-only/RImageBook以下に置く必要がある。
話は変わるが、たとえ、現在のディレクトリが/home/usernameだとしても、readImageのファイルは、/home/username/R/i686-pc-linux-gnu-library/2.14/RImageBookから呼び出しているので、lena.tifの場所は/home/username/R/i686-pc-linux-gnu-library/2.14/RImageBook/images/lena.tifである。
なので、lena.tifを読み込むときには、
readImage(system.file("images/lena.tif", package="RImageBook"))とする。
こんな感じ。
username@username $ sudo R
[sudo] password for th4:
R version 2.14.1 (2011-12-22)
> library(RImageBook)
要求されたパッケージ EBImage をロード中です
要求されたパッケージ abind をロード中です
要求されたパッケージ biOps をロード中です
> lena <- readImage(system.file("images/lena.tif", package="RImageBook"))
> display(lena)
> getwd()
[1] "/home/username"
setwdとかやってもダメのようである。
確率的最急勾配法
1つのwのみ。
#確率的最急勾配法 f<-file("rnorm_data.txt","r") data=function(){ a<-readLines(con=f,1) b=unlist(strsplit(a, "\\,")) # 文字 "," で分割 return(as.numeric(b)) } #data()#ファイルの1行目が読み込まれる #data()#ファイルの2行目が読み込まれる r=0.01 #学習係数の決め方は,難しい。 epsilon=0.00001 end=0 cnt=0 N=10000 #初期値 w=data() f<-file("rnorm_data.txt","r") for(cnt in 1:N){ if(end==0){ #初期値 x=data()#N(0,1)の乱数 y=w%*%x w_previous=w w=w_previous+r*y*(x-y*w_previous) cat("cnt==",cnt,":\n") cat(w,"\n") cat(w_previous,"\n") if((w-w_previous)%*%(w-w_previous)<epsilon){ end=1 cat("(w-w_previous)%*%(w-w_previous)<epsilon\n") cat(w,"\n") cat(w_previous) }else if(cnt==N){ cat("cnt==1000\n") cat(w,"\n") cat(w_previous) } } } close(f)
を求める。
#確率的最急勾配法 f<-file("rnorm_data.txt","r") data=function(){ a<-readLines(con=f,1) b=unlist(strsplit(a, "\\,")) # "," で分割 return(as.numeric(b)) } #data()#ファイルの1行目が読み込まれる #data()#ファイルの2行目が読み込まれる r=0.01 epsilon=0.00001 end=0 end_list=list(0,0,0,0,0) end_cnt_list=list(0,0,0,0,0) cnt=0 N=1000 #初期 w1=data() w2=data() #w2=rnorm(5) w3=data() #w3=rnorm(5) w4=data() #w4=rnorm(5) w5=data() #w5=rnorm(5) w_list=list(w1,w2,w3,w4,w5) w_list y1=numeric(5);y2=numeric(5);y3=numeric(5);y4=numeric(5);y5=numeric(5) y_list=list(y1,y2,y3,y4,y5) numeric=numeric(5) w_previous_list=list(numeric,numeric,numeric,numeric,numeric) w_previous_list w_conv_list=list(numeric,numeric,numeric,numeric,numeric)#wが収束した時のリスト f<-file("rnorm_data.txt","r") for(cnt in 1:N){ #初期値 x=data()#N(0,1)の乱数 for(i in 1:5){ if(end_list[[i]]==0){#収束していないwについて処理する y_list[[i]]=w_list[[i]]%*%x w_previous_list[[i]]=w_list[[i]] orthogonal=numeric(5) if(i>=2){ for(k in 1:5){ if(end_list[[k]]==1){#収束した時(end_list[[k]]==1)収束したものを使う w_conv=w_conv_list[[k]] for(j in 1:(i-1)){# y_list[[j]]=w_conv%*%x orthogonal=orthogonal+y_list[[j]]*w_conv } }else{ for(j in 1:(i-1)){# y_list[[j]]=w_list[[j]]%*%x orthogonal=orthogonal+y_list[[j]]*w_list[[j]] } } } } w_list[[i]]=w_previous_list[[i]]+r*y_list[[i]]*(x-y_list[[i]]*w_previous_list[[i]]-2*orthogonal) cat("i==",i,"::") cat("cnt==",cnt,":\n") cat(w_list[[i]],"\n") cat(w_previous_list[[i]],"\n\n") if((w_list[[i]]-w_previous_list[[i]])%*%(w_list[[i]]-w_previous_list[[i]])<epsilon){ w_conv_list[[i]]=w_list[[i]] end_list[[i]]=1 end_cnt_list[[i]]=cnt cat("w_",i,"is convergence.(cnt=",cnt,")\n") cat("(w_list[[i]]-w_previous_list[[i]])%*%(w_list[[i]]-w_previous_list[[i]])<epsilon\n") cat((w_list[[i]]-w_previous_list[[i]])%*%(w_list[[i]]-w_previous_list[[i]]),"\n\n") cat(w_list[[i]],"\n") cat(w_previous_list[[i]],"\n\n") }else if(cnt==N){ cat("Not Covergence\n") cat("cnt==",N,"\n") cat(w_list[[i]],"\n") cat(w_previous_list[[i]]) } } } } end_list end_cnt_list close(f)
rnorm()によるデータ作成
getwd() setwd("作業ディレクトリ") N=1000 out <- file("rnorm_data.txt", "w") # 書き込みモードで開く for(cnt in 1:N){ x=rnorm(5) for(i in 1:length(x)){ if (i < 5) writeLines(paste(x[i]),out,sep=", ") else if(i==5) writeLines(paste(x[i]),out,sep="\n") } } close(out) # ファイルを閉じる
1行ずつ読み込み
( x <- read.table("rnorm_data.txt") ) f<-file("rnorm_data.txt","r") a<-readLines(con=f,1) a b=unlist(strsplit(a, "\\,")) # "," で分割 mode(b) c=as.numeric(b)
双方な分布のネゲントロピーに関する考察
分布を平均0,分散1にしたときのネゲントロピーを計算し,横軸が0.001刻みで
を0から1まで動かし,縦軸がネゲントロピーの近似した図
(ちゃんとやったのに図が間違っているかも?)

ネゲントロピーが大きいという事はガウス分布から形状が離れているという事である。そこでどういう意味で形状が離れているかという話で,最も分布が双方になった時,つまり,のときに最大であって欲しかったわけだが,そうではない(らしい)。(図が間違っているのかも?)
あたりで最大なので,対称性からのズレか?
間違っていると思うので,誰か教えてください(^_^;)
- コード
#mu*3*phi(3*x) + (1 - mu)*3*phi(3*(x - 1))を平均0分散1にしたときのネゲントロピーの計算 phi=function(x) dnorm(x,mean=0,sd=1) p = function(x){ mu*3*phi(3*x) + (1 - mu)*3*phi(3*(x - 1)) } mu=0 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 pdf=function(x){ p(sqrt(var)*x+mean)*(sqrt(var)) } integrate(pdf,-Inf,Inf) #双方な分布のグラフ xi=seq(-50,50,length=1000) for( mu in 0:10){ mu = mu*0.1 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 plot(xi,pdf(xi),xlab="xi",xlim=c(-5,3),ylim=c(0,0.8),type="l",col=mu*10,lwd=1) par(new=T) } par(new=T) plot(xi,phi(xi),xlab="xi",xlim=c(-5,3),ylim=c(0,0.8),type="o",col=1,lwd=2) par(new=T) mu = 0.2 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 plot(xi,pdf(xi),xlab="xi",xlim=c(-5,3),ylim=c(0,0.8),type="l",col=mu*10,lwd=2) par(new=T) mu = 0.8 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 plot(xi,pdf(xi),xlab="xi",xlim=c(-5,3),ylim=c(0,0.8),type="l",col=mu*10,lwd=3) par(new=T) mu = 0.5 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 plot(xi,pdf(xi),xlab="xi",xlim=c(-5,3),ylim=c(0,0.8),type="l",col=mu*10,lwd=4) e1=function(x){ x*pdf(x) } e2=function(x){ x^2*pdf(x) } integrate(e1,-Inf,Inf) integrate(e2,-Inf,Inf) #gauss=function(x) dnorm(x,mean=1-mu,sd=sqrt((1+7*mu-4*mu^2)/4)) k1=36/(8*sqrt(3)-9) k2a=1/(2-6/pi) #g1:奇関数 g1=function(x){ x*exp(-(x^2)/2)*pdf(x) } #g2a:偶関数 g2a=function(x){ abs(x)*pdf(x) } integrate(g1,-Inf,Inf)$val integrate(g2a,-Inf,Inf)$val mu=0 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 Ja(mu) mu=1 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 Ja(mu) for(mu in 0:1000){ mu = mu*0.001 mean=1-mu var=((10-9*mu)/9)-(1-mu)^2 plot(mu,Ja(mu),xlab="mu",xlim=c(0,1),ylim=c(0,0.08),type="p",lwd=1) par(new=T) }
一般化ガウス族のネゲントロピーに関する考察
#一般化ガウス族(GGF) p=function(xi){ (1/(2*a^(1/a-1)*gamma(1/a)))*exp(-abs(xi)^a/a) } a=2 mean=(a^(1/a))*(gamma(2/a)/gamma(1/a)) var=(a^(2/a))*(gamma(3/a)/gamma(1/a))-((a^(1/a))*(gamma(2/a)/gamma(1/a)))^2 Gauss = function(x){ (1/sqrt(2*pi*(var)^2))*(exp(-((x-(mean))^2)/(2*var^2))) } xi=seq(-50,50,length=1000) default.par <- par() mai <- par()$mai mai[4] <- mai[1] par(mai = mai) for( a in 20:1000){ a = a*0.1 plot(xi,p(xi),xlab="xi",xlim=c(-4,4),ylim=c(0,1),type="l",col=a*10) par(new=T) } a=1000 par(new=T) mean=(a^(1/a))*(gamma(2/a)/gamma(1/a)) var=(a^(2/a))*(gamma(3/a)/gamma(1/a))-((a^(1/a))*(gamma(2/a)/gamma(1/a)))^2 plot(xi,Gauss(xi),xlab="xi",ylab="",xlim=c(-4,4),ylim=c(0,4.5), axes = FALSE,type="l") axis(4) mtext("Gauss", side = 4, line = 3) par(default.par) #確率1かぁ? integrate(Gauss,-Inf,Inf)
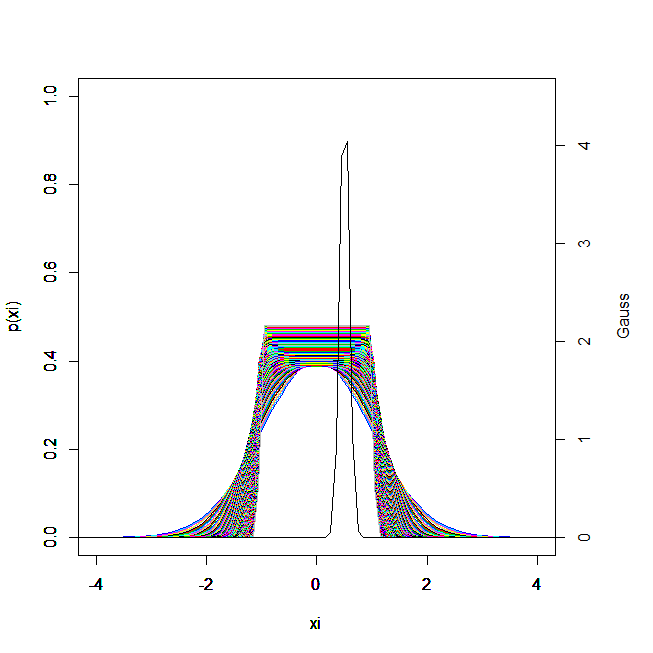
for( a in 20:1000){ a = a*0.1 mean=(a^(1/a))*(gamma(2/a)/gamma(1/a)) var=(a^(2/a))*(gamma(3/a)/gamma(1/a))-((a^(1/a))*(gamma(2/a)/gamma(1/a)))^2 plot(xi,Gauss(xi),xlab="xi",ylab="Gauss",xlim=c(-4,4),ylim=c(0,5),type="l" ,col=a*10) par(new=T) }

一般化ガウス族のネゲントロピーはaをにすると,とても大きくなります。
ネゲントロピーが大きいということは,その分布の持つ平均と分散をもつようなガウス分布と見た目から別の形をしていることが言える。
今の場合一般化ガウス族でのaをにすると、一様分布になるので明らか。
2軸の書き方は、以下を参考にした。
http://d.hatena.ne.jp/teramonagi/20120107/1325922512