指数べき乗分布の尖度

さて、指数べき乗分布に関する考察は今回で一旦終わりにしますが、
の指数べき乗分布の尖度の挙動を見たいと思います。

> for(v in 1:20){
+ v=v*0.1
+ printf("v=%f\n",v);
+ cat(gamma(1/v)*gamma(5/v)/(gamma(3/v))^2-3,"\n\n")
+ }
v=0.100000
2823513 

v=0.200000
1956.297 

v=0.300000
170.9691 

v=0.400000
48.95105 

v=0.500000
22.2 

v=0.600000
12.57877 

v=0.700000
8.062091 

v=0.800000
5.565144 

v=0.900000
4.02557 

v=1.000000
3 

v=1.100000
2.276601 

v=1.200000
1.743484 

v=1.300000
1.336812 

v=1.400000
1.017863 

v=1.500000
0.7619542 

v=1.600000
0.5526952 

v=1.700000
0.3788198 

v=1.800000
0.2323545 

v=1.900000
0.1075123 

v=2.000000
-4.440892e-16 

2のときの入れましたが。。

ちなみに2のときはガウス分布に従います。誤差が出てますが、ものすごい小さいのでいいでしょう。
また1のときはラプラス分布です。ちゃんと尖度が3ですね。

今度はのとき、

> #----------------------------
> for(v in 2:1000){
+ printf("")
+ #v=v*0.1
+ printf("v=%f\n",v);
+ cat(gamma(1/v)*gamma(5/v)/(gamma(3/v))^2-3,"\n\n")
+ }

v=2.000000
-4.440892e-16 

v=3.000000
-0.5816008 

v=4.000000
-0.8115604 

v=5.000000
-0.9299017 

v=6.000000
-1 

v=7.000000
-1.045368 

v=8.000000
-1.07659 

v=9.000000
-1.099073 

v=10.000000
-1.115841 

v=11.000000
-1.1287 

v=12.000000
-1.13879 

v=13.000000
-1.14686 

v=14.000000
-1.153419 

v=15.000000
-1.158825 

v=16.000000
-1.163335 

v=17.000000
-1.167138 

v=18.000000
-1.170376 

v=19.000000
-1.173154 

v=20.000000
-1.175558 

v=21.000000
-1.177651 

v=22.000000
-1.179486 

v=23.000000
-1.181102 

v=24.000000
-1.182534 

v=25.000000
-1.183809 

v=26.000000
-1.184948 

v=27.000000
-1.185971 

v=28.000000
-1.186893 

v=29.000000
-1.187727 

v=30.000000
-1.188484 

v=31.000000
-1.189172 

v=32.000000
-1.1898 

v=33.000000
-1.190375 

v=34.000000
-1.190903 

v=35.000000
-1.191389 

v=36.000000
-1.191836 

v=37.000000
-1.192249 

v=38.000000
-1.192632 

v=39.000000
-1.192987 

v=40.000000
-1.193317 

v=41.000000
-1.193624 

v=42.000000
-1.193911 

v=43.000000
-1.194178 

v=44.000000
-1.194429 

v=45.000000
-1.194663 

v=46.000000
-1.194883 

v=47.000000
-1.19509 

v=48.000000
-1.195284 

v=49.000000
-1.195467 

v=50.000000
-1.195639 

#中略

v=1000.000000
-1.199988 

#中略

v=10000.000000
-1.2 

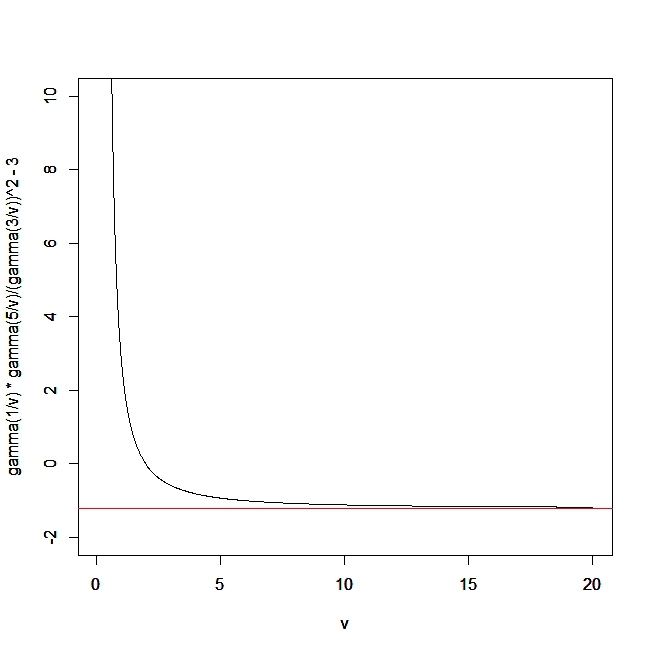
最小は-1.2かな？

追記：(12.6.3)
vを無限大にすると一様分布に従うんだから、一様分布の尖度は-1.2だから、こうなるんだね。

その時は、気が付かなかった。

追記終わり

結果として、
のときは、尖度が正の値なので、優ガウス的密度。
のときは、尖度が負の値なので、劣ガウス的密度。

v=2の時はガウス分布なので0です。

ならなかったら、がっかりでしたがちゃんと出来ました。

ちょっと気になったので、2に近いところでの挙動を見てみました。

for(v in 19000:20000){
	v=v*0.0001
	printf("v=%f\n",v);
	cat(gamma(1/v)*gamma(5/v)/(gamma(3/v))^2-3,"\n\n")
}

v=1.999000
0.001000702 

v=1.999100
0.0009005682 

v=1.999200
0.0008004489 

v=1.999300
0.0007003437 

v=1.999400
0.0006002525 

v=1.999500
0.0005001753 

v=1.999600
0.0004001122 

v=1.999700
0.0003000631 

v=1.999800
0.000200028 

v=1.999900
0.000100007 

v=2.000000
-4.440892e-16 

vが1.999900から2までの値の減り方がヤバス。

6/7追記：

v=seq(0.1,20,,1000)
plot(v,gamma(1/v)*gamma(5/v)/(gamma(3/v))^2-3,xlim=c(0.1,20),ylim=c(-2,10),type="l")
par(new=T)
abline(h = -1.2,col="red")

図を書いたほうが良かったですね。

赤い水平軸が-1.2のところを表しています。何回も言いますが、vを無限大にするとpdfは一様分布になるからです。