独立成分分析について

詳解 独立成分分析―信号解析の新しい世界

入門 独立成分分析

特にFastICAについて。FastICAは、独立成分分析の中のアルゴリズムでは最も優れている(らしい)。収束性や誤差の意味で。確かに勾配法だと、洒落にならないくらい計算時間がかかるし、かなりの誤差が多々ある。

• 独立成分分析は何ができるか？

混合されているデータの分類または復元です。

例えば、音声はだいたい以下のの画像の上部の2つのような分布になります。
今はシュミレーションのため、優ガウス分布のラプラス分布を上部に、下部に一様分布を書きました。(源信号とする)

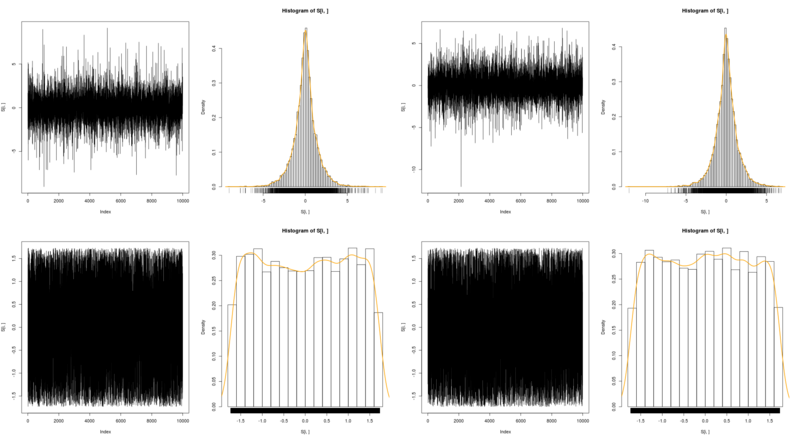
これら4つの信号を混合したデータから、源信号を復元したいと思います。
つまり、源信号(人の話し声)が、混ざり合った状態からそれぞれの声に分類するということになります。

モデルは、

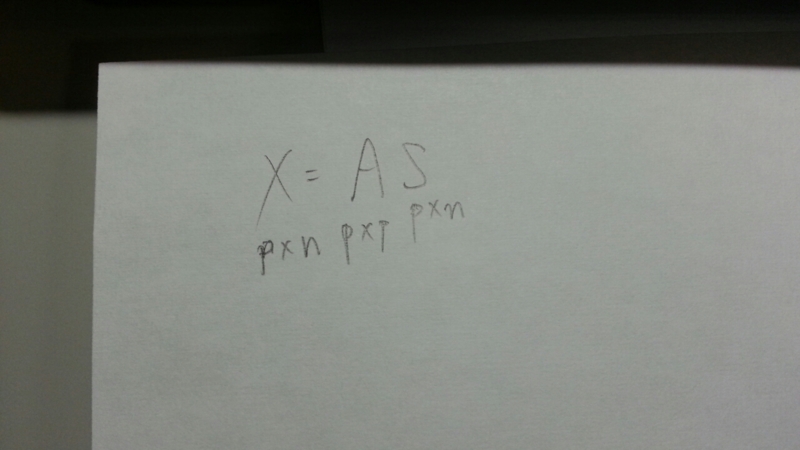
になります。
(p:次元数,n:標本数)
Xが観測データだと考えることになります。

Xの情報から、未知のAとSを見つける必要があります。

Xは、Sの混合なので、元の非ガウス分布よりもガウス分布に近づいています。(中心極限定理より)

独立成分分析は、ガウス分布をより非ガウス分布に近づけることで、源信号の復元を可能にしています。
その際、非ガウス性の尺度として、尖度やネゲントロピーを用います。ちなみに、尖度は外れ値に関して頑健でないので、ネゲントロピーを使いましょう。

また、前処理として白色化(無相関化)をすることで、より独立な状態に近づけています。

白色化については、以下参照。
白色化 - 機械学習の「朱鷺の杜Wiki」

実際、以下のコードによって復元したデータのヒストグラムを書いてみると、以下のようになります。

すばらしいですね。

実際の音声データでは、時間相関がある場合があり、その点を考慮しなければなりません。

mathematicaで書いていたが、データセットの扱いで問題があったので、新たにRで書きなおしました。

スター下さい。

参考:Cocktail party demo

#複数の独立成分を推定するfastICA

library(splus2R);
library(VGAM);

source("signaldata.R");
source("fastICA_func.R");


n=10000 #標本数
p=4 #独立成分の数
S1<-signaldata("laplace",2,n) #row:2,col:n
S2<-signaldata("unif",2,n) #row:2,col:n
S<-rbind(S1,S2) #row:4,col:n

plot(S[1,],type="l")
hist(S[1,],breaks="Scott",freq = FALSE)
lines(density(S[1,]), col = "orange", lwd = 2)
rug(S[1,])

#混合行列の作成
A<-matrix(runif(p^2,-sqrt(3),sqrt(3)),p)
A<-t(A)
dim(A)

#観測データXの作成
X=A%*%S #p,n
dim(X)
X<-X-apply(t(X),2,mean) #
plot(X[1,],type="l")
hist(X[1,],breaks="Scott",freq = FALSE)
lines(density(X[1,]), col = "orange", lwd = 2)
rug(X[1,])

X<-t(X)



###################

m=4 #独立成分の数

result<-fastICAmult(X,m)
V<-result$V
dim(V)

W<-result$W
W

Z<-result$Z

t(W)%*%V%*%A #順序行列になれば成功


restoredsignal<-result$restoredsignal

par(mfrow=c(2,2))
for(i in 1:4){
    hist(restoredsignal[i,],breaks="Scott",freq = FALSE)
    lines(density(restoredsignal[i,]), col = "orange", lwd = 2)
    rug(restoredsignal[i,])
}

signaldata.R

library(VGAM);
signaldata <-function(func,p,n){
    S<-matrix(0,p,n); #n*p
    i=1;
    while(i<=p){
        if(func == "unif"){
            u<-runif(n,-sqrt(3),sqrt(3));
        }else if(func == "laplace"){
            u<-rlaplace(n, location=0, scale=1);
        }else if(func == "norm"){
            u<-rnorm(n);
        }
        S[i,]<-u;
        i<-i+1;
    }
    return(S);
}

fastICA_func.R

fastICAmult<-function(X,m,W=signaldata("unif",m,m),maxcnt=10000,epsilon=0.0001){
    if(dim(X)[2]>dim(X)[1]){ #行:signal,列:標本
        X<-t(X);
    }
    
    V<-svd(var(X))$u%*%diag(1/sqrt(svd(var(X))$d))%*%t(svd(var(X))$u);
    Z<-V%*%t(X); #whitening
    #Z=V%*%X #ok
    #W <- matrix(scan("W_init01.txt"), nrow=m) #ok
    W<-t(W)
    #ノルム1にする
    for(i in 1:m){
        W[,i]<-W[,i]/vecnorm(W[,i])
    }
    i=1;
    while(i<=m){
        cat("Independent Component:",i,"\n");
        cnt=0;
        while(cnt<maxcnt){
            #cat("cnt:",cnt,"\n")
            #5.
            wbefore<-W[,i]
            W[,i]<-apply(t(t(Z)*tanh(t(W[,i])%*%Z)[1,]),1,mean)-mean(1-(tanh(t(W[,i])%*%Z)[1,])^2)*W[,i];
            #6.グラムシュミットの直交化
            if(2<=i){
                Sum=0;
                for(j in 1:(i-1)){
                    Sum<-Sum+(t(W[,i])%*%W[,j])*W[,j];
                }
                W[,i]<-W[,i]-Sum; #2<=i
            }
            #7.収束したか?
            W[,i]<-W[,i]/vecnorm(W[,i]);
            #cat("W[,i]:",W[,i],"\n\n")            
            if(1-epsilon<=abs(t(wbefore)%*%W[,i]) && abs(t(wbefore)%*%W[,i])<=1+epsilon){
                cat("cnt:",cnt,"\n");
                cat("W[,i]:",W[,i],"\n\n");
                i<-i+1;
                cnt=maxcnt;
            }
            cnt=cnt+1;
        }
    }
    
    return(list(V=V,W=W,Z=Z,restoredsignal=as.matrix(t(W)%*%Z[,1:n])))
}